优化求解器 | Gurobi 数学启发式算法:参数类型与案例实现
作者:徐璐,清华大学,清华大学深圳国际研究生院,清华-伯克利深圳学院,硕士在读
作者:刘兴禄,清华大学,清华大学深圳国际研究生院,清华-伯克利深圳学院,博士在读
审校&编辑:张瑞三,四川大学,硕士在读
初次完稿日期:2022.10.12
启发式算法通常能够以巧妙、迅速的方式快速解决问题,在运筹学中有着不可取代的地位。今天我们着重探究其中的数学启发式算法,尤其是 Gurobi 求解器中提供的启发式,以及涉及到的重要参数。在本文的最后,我们以经典的 VRPTW 案例为例详细列举了8类参数的实际应用情况,提供真实完整的运行日志供大家参考。
本文的结构如下:
- Part1:数学启发式算法
- Part2:Gurobi 数学启发式算法的类型和特点
- Part3:Gurobi 数学启发式算法相关参数介绍
- Part4:实验:各参数取值和基于 VRPTW 的案例
什么是启发式算法?在数学优化和计算机科学中,启发式 heuristic(来自希腊语ε?ρ?σκω 「我发现,发现」)是一种旨在当经典方法太慢时用来更快解决问题的技术,或者无法通过经典方法找到精确解时用来获得近似解决方案的方法。它是通过用最优性、完整性、精确性换取速度来实现的。在某种程度上,可以被认为是一种捷径。(来自 wikipedia)
那么数学启发式 matheuristic 又是什么呢?正如其命名所言,它是数学规划算法和启发式或元启发式算法的有机结合,如下示意图所示:
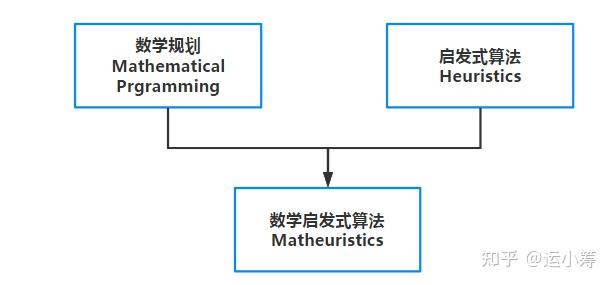
数学启发式算法相比元启发式算法,理论性更强。数学启发式往往会借助一部分数学规划提供的解,或者问题的特性等,来快速获得问题的可行解。本文主要聚焦于介绍在Gurobi求解器中,用于加速求解混合整数规划(Mixed integer programming, MIP)的数学启发式算法。
在 Gurobi 求解器中,整个算法依然是以数学规划为框架,仅在其中的某些环节采用了启发式算法,以达到更快获得初始可行解、更多或更优质的可行解等各种目的。Gurobi求解MIP的算法框架为 branch and cut,但是在 branch and cut tree 的探索中,在每个节点处,会调用30多种启发式算法,用于快速获得高质量的整数可行解,进而加速上界(min 问题)的更新Gap的收敛。此外,每个节点上也会调用二十多种 cutting plane 算法来生成割平面,收紧模型,逼近该节点的可行域的凸包,收紧下界。Branch and cut 算法框架中,启发式算法的调用时机如下面示意图所示,启发式算法一般是在红色虚线框部分被调用:
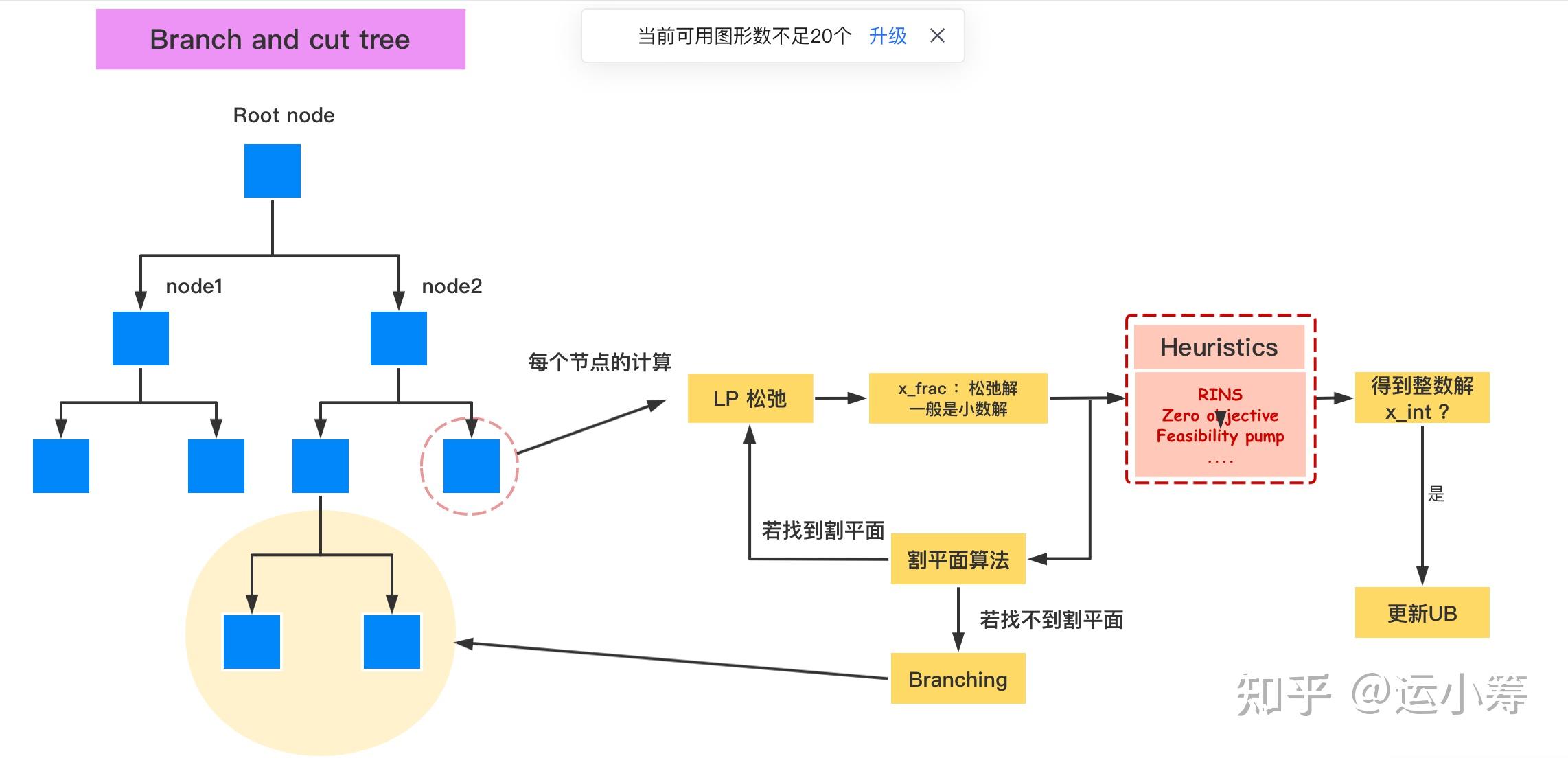
为了让读者看得清楚,我们把每个节点处的算法放大,如下图。
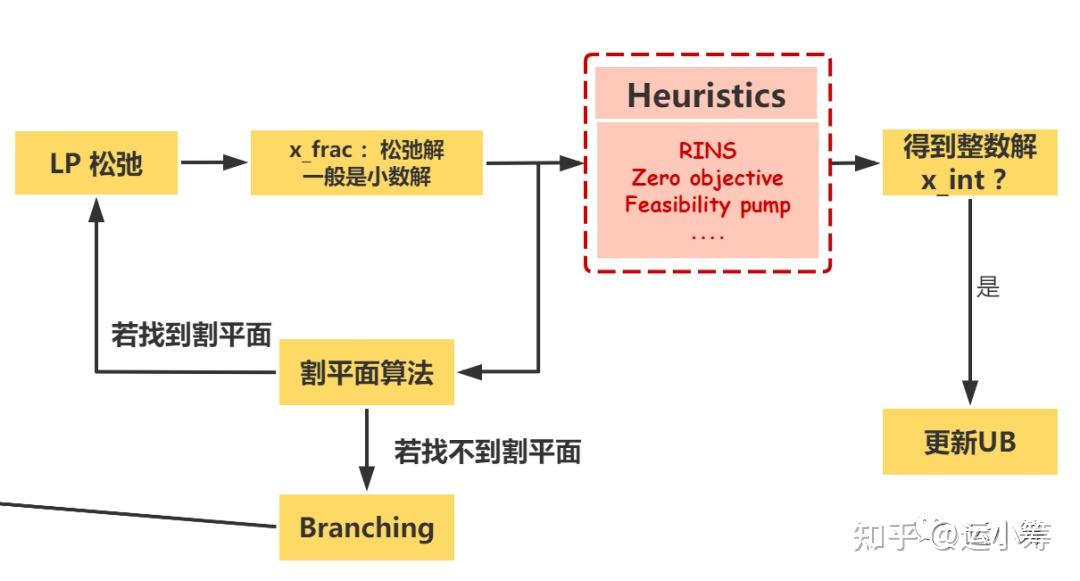
Gurobi 提供了超过30种启发式算法,包含以下多种类型:
-[ ]基于非 LP(Non-LP based)\\ Enumerate, search, greedy, ... -[ ]基于 LP(LP based)\\ Rounding, fixing & diving, ... -[ ]模型改建(Reformulation)\\ Zero-objective, min relaxation, ... -[ ]改进型(Improvement)\\ RINS -[ ]子 MIP 和递归(SubMIP and recursive)\\ Target heuristic, RINS, ... -[ ]针对具体问题的启发式(Problem specific)\\ Fixed charge network heuristic -[ ]有助于启发式的功能(Featureshelpingheuristics)\\ Pump reduce
- 基于非 LP(Non-LP based)
Enumerate, search, greedy, ...
- 基于 LP(LP based)
Rounding, fixing & diving, ...
- 模型改建(Reformulation)
Zero-objective, min relaxation, ...
- 改进型(Improvement)
RINS
- 子 MIP 和递归(SubMIP and recursive)
Target heuristic, RINS, ...
- 针对具体问题的启发式(Problem specific)
Fixed charge network heuristic
- 有助于启发式的功能(Featureshelpingheuristics)
Pump reduce
- 其中比较著名的算法包括:
最优的(Optimal):最短路径(shortest path),最小生成树(min spanning tree)\\ 非最优的(Not optimal):0-1 Knapsack 0-1 背包问题
根据目标系数和约束系数的比例对变量进行排序,已经排序的变量。 根据顺序将变量取值逐一设为1,直到产生不可行解。例如这里将
设置为1是不可行的,所以解是
,目标值为29。 而最优解
,目标值为30。
2. Gurobi 盲目启发式(这里的盲目意味着不使用 LP 松弛解)
这一类启发式算法的求解步骤通常如下:
- 首先,基于某种度量对二进制/整数变量进行排序;
- 接着,按贪婪顺序固定这些变量;
- 然后,传播变量固定和收紧界值:
注意如果没有这一步,几乎不可能找到可行解。
最后如果有连续变量的话,解决剩余的 LP 模型。
3. 基于 LP 的贪婪算法(LP based greedy heuristics) 这类算法具有以下特点:
- 用松弛解对变量排序通常更有效;
- 有可能可以快速找到整数解;
- 解的质量通常很差;
- 一个差的解 就足够了, 差的解往往无法帮助整体优化;
- 多核电脑和难以对根节点并行化是关注基于非LP的启发式算法的原因
- 取整法(Rounding)
基本思想:解 LP 松弛问题,将解值四舍五入到最接近的整数值。
举例说明:这里我们举和前文相同的 0-1背包例子: 最优的 LP 松弛解
,利用取整法可得
,这是一个整数可行解,目标函数值为29。
值得注意的是,简单的取整法通常表现不是很好,特别是具有等式约束的模型。除此之外,往往需要考虑两边的整数值,取整时需要传播变量固定和收紧界值。Gurobi 求解器里有多种不同版本的取整启发式算法。
2. 大多数 Gurobi 启发式算法都是基于 LP 或需要 LP 松弛解
LP 松弛解对于启发式算法获取高质量解非常重要!
1.举例,原模型如下:
2.去目标的启发式
首先删除目标函数并将其作为可行问题去求解,以期预优化可以使模型变的更小,并且最终的预优化模型更容易解。 这个启发式算法一般只在根结点使用。
对于上述例子,重新改建的模型是:
变量
和
是平行的,
可以被固定为0,变量
可以被固定为1,这有助于第一个约束的可行性。
3.最小松弛启发式算法
算法步骤如下:
- 首先,对于每个不等式,加一个违反约束的惩罚变量;
- 接着,对于每个等式,加两个违反约束的惩罚变量, 两个方向各一个;
- 然后对违反约束总和求最小化;
- 如果最优总和为0, 那我们找到一个可行解; 否则原始模型是不可行的。
继续上述例子,重新改建的模型是:
1.RINS 的求解过程 RINS 全称是 Relaxation induced neighborhood search,即松弛诱导邻域搜索。其求解的流程如下:
- 首先,给定现任整数解(目前找到的最优整数解)和节点松弛的当前分数解;
- 如果变量的整数解值和松弛解值一致,则固定变量;
- 最后将部分固定的模型作为 subMIP 去解。
RINS 是一种改进型的启发式算法,是公认的最有效的一种启发式算法。
许多Gurobi启发式算法会这样做:
- 首先,设一个目标来固定一定比例的变量,比如80%;
- 接着,固定一个变量然后传播;
- 重复固定和传播,直到达到目标或它变得不可行;
- 然后将其为 subMIP 去求解;
- 在子MIP中,它将以递归方式调用相同的启发式算法。
这种方法通常非常有效,可迅速找到可行解。
泵式缩减启发式来源于 Fischetti,Glover 和 Lodi 在 2004 的研究成果,其求解步骤如下:
- 首先,将目标函数换成到舍入整数解距离最小 (二次);
- 接着,使用 L1 范数
, 其中
是取整解(线性)
如果一个二元变量 ,那么
,那么
的目标部分为
,即目标函数系数为1;
如果一个二元变量 ,那么
,那么目标函数系数将为 -1。
- 解修改后的LP并重复;
- 直到它达到一定限值或松弛解是整数可行的;
- 例如将限值设为10, 则需解 LP 10 次, 这是一个很花费时间的过程,并且通常很难运气好。
泵式缩减法受泵式缩减启发式算法的启发,这种算法基于一个观察:大多数模型是对偶退化的,即松弛问题有多个的最优解。 泵式缩减法的目标是找到有较少整数变量取分数值的松弛解,其主要步骤如下:
- 首先,解松弛问题, 固定非零递减成本的所有变量, 确保保持在最优空间;
- 接着,舍入松弛解,目标换成到舍入整数解距离最小 (L1 范数);
- 然后,解修改后的 LP 并重复;
- 直到它达到一定限值或取小数值的整数变量的数量不下降。
Gurobi 求解器主要包含以下四类参数:
- MIPFocus:主要 MIP 参数(Main MIP parameter)
2. Heuristics:主要启发式参数(Main heuristic parameter)
3. 个别启发式参数(Individual heuristic parameters)
- ZeroObjNodes:去目标启发式(Zero objective heuristic)
- PumpPasses:泵式缩减启发式(Feasibility pump heuristic)
- RINS:松弛诱导邻域搜索启发式(RINS heuristic)
- SubMIPNodes:限制基于MIP的启发式方法(如RINS)所探索的节点数量
- 节点松弛启发式(Node relaxation heuristic):MinRelNodes:最小松弛启发式(Minimum relaxation heuristic),NoRelHeurTime::节点松弛启发式的运行时间和NoRelHeurWork:节点松弛启发式的计算量限制
- 改进型的启发式参数(Improvement heuristic parameters): ImproveStartGap,ImproveStartNodes和ImproveStartTime
4. 影响可行解的其他参数(Other parameters affecting feasible solutions)
- BranchDir:分支方向的偏好。将这个参数设定为1,可能有助于 MIP 更迅速地找到可行解。
- TuneCriterion 调优准则。=2 表示为目标函数值,即更专注于寻找好的可行解。
- PartitionPlace:分割位置。
下一节我们将结合具体的案例逐一详细介绍每一类参数的取值,通过运行日志比较运行结果。
这一节中,我们将基于一个 VRPTW 案例来具体演示上述参数。
VRPTW的问题介绍和模型见往期推文(第一个即为VRPTW,其余两个为相关学拓展学习推文):
优化| 手把手教你用Python调用Gurobi求解VRPTW优化 | 两阶段启发式算法求解带时间窗车辆路径问题(附Java代码)优化 | 手把手教你用C++调用Gurobi求解CVRP:环境配置、数学模型及完整代码有关带时间窗的车辆路径规划问题(VRPTW 问题),简单来说就是在传统的 VRP 问题上增加了时间窗的约束。网络中每个节点对车辆都有一个期望的最早抵达与最晚抵达的时间窗约束,车辆必须在规定的时间窗内到达每个节点,若违反时间窗约束会产生惩罚项。
其他部分则与普通VRP相同,目标函数都是最小化总成本,决策变量考虑的都是车辆的调度路径 。
下文实验中我们放上了每个参数下 Gurobi 求解的完整运行日志,因此内容较长,读者朋友们可以按需阅读。
from gurobipy import *
model = read("VRPTW_r102_20_5.mps")笔者注:如果大家想要查看这个 .mps 文件中 VRPTW 模型的细节(如目标函数和约束条件),可以将其导出为 .lp 格式:
model.write("vrp.lp")再用 NotePad++ 等软件打开查看,该模型文件共有 3960行,共 1796 个约束:

我们首先不添加任何参数,直接让 Gurobi 按照所有默认的参数取值进行求解:
model = read("VRPTW_r102_20_5.mps")
model.optimize()运行日志如下:
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.02 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.10s
Presolved: 1183 rows, 1519 columns, 16772 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Root relaxation: objective 2.871000e+02, 410 iterations, 0.03 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 37 - 287.10000 - - 0s
0 0 287.10000 0 59 - 287.10000 - - 0s
0 0 287.10000 0 64 - 287.10000 - - 0s
0 0 304.71668 0 83 - 304.71668 - - 0s
0 0 332.21792 0 82 - 332.21792 - - 0s
0 0 332.21792 0 85 - 332.21792 - - 0s
0 0 335.90452 0 80 - 335.90452 - - 0s
0 0 337.50589 0 95 - 337.50589 - - 0s
0 0 337.52434 0 92 - 337.52434 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 1s
0 0 343.62317 0 95 - 343.62317 - - 1s
0 0 349.99973 0 105 - 349.99973 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 356.60000 0 73 - 356.60000 - - 1s
0 0 356.60000 0 98 - 356.60000 - - 1s
0 0 357.53333 0 61 - 357.53333 - - 1s
H 0 0 461.2000000 357.53333 22.5% - 1s
0 0 357.53333 0 59 461.20000 357.53333 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.77309 0 118 461.20000 357.77309 22.4% - 1s
0 0 357.77309 0 109 461.20000 357.77309 22.4% - 1s
0 2 357.81724 0 109 461.20000 357.81724 22.4% - 1s
H 33 40 453.1000000 358.10075 21.0% 51.6 1s
H 111 104 449.3000000 358.10075 20.3% 37.8 2s
H 111 104 448.4000000 358.10075 20.1% 37.8 2s
H 139 147 439.2000000 358.10075 18.5% 35.6 2s
H 185 185 429.5000000 358.10075 16.6% 31.2 2s
H 221 219 421.8000000 358.10075 15.1% 28.9 2s
H 409 350 418.4000000 358.10075 14.4% 28.7 3s
1046 764 374.39071 10 38 418.40000 361.05189 13.7% 28.7 5s
1071 781 378.36537 14 91 418.40000 365.45524 12.7% 28.0 10s
1741 943 374.27072 38 80 418.40000 365.45524 12.7% 39.2 15s
4623 2069 386.91601 42 76 418.40000 376.54679 10.0% 41.2 20s
6762 2820 cutoff 49 418.40000 379.88008 9.21% 42.4 25s
8675 3551 cutoff 32 418.40000 383.24012 8.40% 43.5 30s
*12715 4168 44 414.9000000 388.34862 6.40% 44.0 34s
12722 4277 cutoff 59 414.90000 388.36514 6.40% 44.0 35s
*12785 3950 44 412.3000000 388.36514 5.81% 44.1 35s
*13527 3546 57 409.7000000 389.04944 5.04% 44.3 36s
16291 2816 cutoff 73 409.70000 394.84309 3.63% 45.2 40s
Cutting planes:
Gomory: 8
Cover: 46
Implied bound: 25
Clique: 7
MIR: 14
StrongCG: 8
Flow cover: 45
Inf proof: 2
Zero half: 10
RLT: 121
Relax-and-lift: 7
Explored 21289 nodes (910378 simplex iterations) in 44.39 seconds
Thread count was 8 (of 8 available processors)
Solution count 10: 409.7 412.3 414.9 ... 453.1
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%日志的第一列中,若没有任何标注则表示在当前节点未找到新的整数可行解,标注 H 表示当前节点使用使用启发式算法找到了新的可行整数解,标注 * 的为使用经典割平面法且找到了新的可行整数解。可以发现,在 Gurobi 的默认求解过程其实就使用了很多次数学启发式。
日志显示,求解过程使用启发式算法在1s时找到了初始可行整数解,目标函数值为 461.2。在探索了 21289 个节点,共计耗时 44.9s 后找到了最优解,目标函数值为 409.7。
我们重复了3次试验,在这3次中分别使用了 44.4s, 39.1s,38.9s 找到最优解,目标函数值均为 409.7。
MIPFocus 参数用于定义解的高层次策略,因为求解 MIP 问题主要有三个侧重点:侧重快速找到可行解、侧重证明最优、以及侧重界的提升。可以通过本参数设定 MIP 求解的侧重点。注意该参数只会影响 MIP 问题的求解:

- 默认值=0,为在找新的可行解和证明最优性之间取得平衡;
- =1:更注重快速找到可行解(good feasible solution);
- =2:更注重证明最优性(optimal solution),认为求解器在寻找高质量的解方面没有问题,希望将更多的注意力集中在证明最优性上;
- =3:更注重目标界值(bound),如果最佳目标边界移动非常缓慢(或根本没有)。
接下来我们加入参数,先取 MIPFocus=1,更注重快速找到可行解:
model = read("VRPTW_r102_20_5.mps")
model.setParam("MIPFocus", 1)
model.optimize()运行结果如下:
Using license file C:\\Users\\xuluz\\gurobi.lic
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.02 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Changed value of parameter MIPFocus to 1
Prev: 0 Min: 0 Max: 3 Default: 0
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.08s
Presolved: 1183 rows, 1519 columns, 16772 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Root relaxation: objective 2.871000e+02, 410 iterations, 0.02 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 37 - 287.10000 - - 0s
0 0 287.10000 0 55 - 287.10000 - - 0s
0 0 287.10000 0 51 - 287.10000 - - 0s
0 0 304.71668 0 68 - 304.71668 - - 0s
0 0 304.71668 0 68 - 304.71668 - - 0s
0 0 326.81008 0 91 - 326.81008 - - 0s
0 0 327.87089 0 92 - 327.87089 - - 0s
0 0 327.87089 0 92 - 327.87089 - - 0s
0 0 336.38464 0 90 - 336.38464 - - 0s
0 0 339.02500 0 79 - 339.02500 - - 0s
0 0 339.74664 0 103 - 339.74664 - - 0s
0 0 339.74664 0 103 - 339.74664 - - 0s
0 0 351.84850 0 94 - 351.84850 - - 1s
H 0 0 728.3000000 351.90000 51.7% - 4s
H 0 0 674.1000000 351.90000 47.8% - 4s
0 2 351.90000 0 89 674.10000 351.90000 47.8% - 4s
11 16 375.44052 4 82 674.10000 352.99854 47.6% 102 5s
H 31 36 609.6000000 352.99854 42.1% 83.3 5s
H 34 36 541.0000000 352.99854 34.8% 83.4 5s
H 67 59 506.9000000 352.99854 30.4% 65.0 5s
H 68 59 476.6000000 352.99854 25.9% 64.2 5s
H 110 73 467.9000000 352.99854 24.6% 49.7 5s
H 146 93 452.8000000 353.49470 21.9% 46.3 5s
H 148 93 450.3000000 353.49470 21.5% 45.9 5s
H 187 129 433.2000000 353.49470 18.4% 43.2 6s
H 215 141 427.5000000 353.49470 17.3% 43.5 6s
H 265 155 424.9000000 356.20454 16.2% 42.8 7s
H 340 198 418.1000000 356.25462 14.8% 42.9 7s
H 418 221 409.7000000 356.32544 13.0% 44.5 7s
1500 676 379.49853 10 41 409.70000 361.93614 11.7% 43.1 10s
3020 882 369.59724 33 98 409.70000 362.88443 11.4% 43.4 15s
5048 1021 infeasible 34 409.70000 376.05157 8.21% 44.3 20s
8147 1986 403.54507 48 65 409.70000 381.00849 7.00% 44.2 25s
11479 2869 404.56389 35 41 409.70000 383.18182 6.47% 44.0 30s
15696 3644 infeasible 38 409.70000 386.29375 5.71% 43.5 36s
18587 4046 cutoff 57 409.70000 388.31940 5.22% 42.9 40s
23618 4640 405.44765 44 57 409.70000 390.75254 4.62% 41.9 45s
26207 5028 cutoff 48 409.70000 391.80702 4.37% 41.3 50s
29893 5354 394.57034 49 75 409.70000 393.04075 4.07% 40.8 55s
34569 5516 cutoff 30 409.70000 394.67274 3.67% 40.1 60s
36856 5455 401.18344 49 56 409.70000 395.54757 3.45% 39.8 66s
39249 5444 infeasible 59 409.70000 396.32941 3.26% 39.5 70s
44637 5039 401.18362 40 75 409.70000 398.00000 2.86% 38.8 75s
49999 4280 401.65332 49 67 409.70000 399.62280 2.46% 38.0 80s
52955 3530 cutoff 63 409.70000 400.70717 2.19% 37.5 85s
59530 508 cutoff 45 409.70000 404.24587 1.33% 36.3 90s
Cutting planes:
Learned: 3
Gomory: 2
Cover: 7
Implied bound: 13
Clique: 7
MIR: 10
StrongCG: 8
Flow cover: 38
Inf proof: 3
Zero half: 27
RLT: 140
Relax-and-lift: 4
Explored 61203 nodes (2191495 simplex iterations) in 90.81 seconds
Thread count was 8 (of 8 available processors)
Solution count 10: 409.7 418.1 424.9 ... 506.9
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%该求解过程用了 4s 找到初始可行解,共用了 90.81s 探索了 61203 个节点后找到了最优解。
可以发现在这个测试模型中使用 MIPFocus=1 参数值后,可行解的求解速度不升反降,这也说明启发式参数未必都能在任何情况下都实现预期的效果,需要探索和经验。
再取 MIPFocus=2,这个参数取值更注重证明最优性:
model = read("VRPTW_r102_20_5.mps")
model.setParam("MIPFocus", 2)
model.optimize()运行结果如下:求解器使用了 2s 找到第一个可行整数解,此时 Gap 为 27.6%。在 49.38s 找到最优解。
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.03 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Changed value of parameter MIPFocus to 2
Prev: 0 Min: 0 Max: 3 Default: 0
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.12s
Presolved: 1183 rows, 1519 columns, 17138 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Presolve removed 5 rows and 0 columns
Presolved: 1178 rows, 1519 columns, 16940 nonzeros
Root relaxation: objective 2.871000e+02, 452 iterations, 0.06 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 36 - 287.10000 - - 0s
0 0 288.85996 0 75 - 288.85996 - - 0s
0 0 297.37522 0 68 - 297.37522 - - 0s
0 0 310.32413 0 103 - 310.32413 - - 0s
0 0 310.32413 0 103 - 310.32413 - - 0s
0 0 334.24463 0 95 - 334.24463 - - 1s
0 0 337.42636 0 91 - 337.42636 - - 1s
0 0 341.02966 0 106 - 341.02966 - - 1s
0 0 341.03147 0 85 - 341.03147 - - 1s
0 0 343.33133 0 115 - 343.33133 - - 1s
0 0 345.49622 0 115 - 345.49622 - - 1s
0 0 345.70350 0 103 - 345.70350 - - 1s
0 0 355.47619 0 84 - 355.47619 - - 1s
0 0 355.47619 0 84 - 355.47619 - - 1s
H 0 0 491.0000000 355.47619 27.6% - 2s
0 0 357.06781 0 97 491.00000 357.06781 27.3% - 2s
0 0 358.00000 0 93 491.00000 358.00000 27.1% - 2s
0 0 358.00000 0 89 491.00000 358.00000 27.1% - 2s
0 0 358.00000 0 79 491.00000 358.00000 27.1% - 2s
H 0 0 464.4000000 358.00000 22.9% - 3s
0 0 358.03600 0 118 464.40000 358.03600 22.9% - 3s
0 0 358.03600 0 118 464.40000 358.03600 22.9% - 3s
0 0 358.12398 0 117 464.40000 358.12398 22.9% - 3s
0 0 358.12398 0 117 464.40000 358.12398 22.9% - 3s
0 2 359.17920 0 117 464.40000 359.17920 22.7% - 4s
H 35 37 443.9000000 359.17920 19.1% 51.6 4s
H 64 69 429.3000000 359.17920 16.3% 49.6 4s
91 97 363.56589 20 83 429.30000 359.17920 16.3% 46.3 5s
H 127 116 419.6000000 359.17920 14.4% 42.3 5s
H 157 144 416.2000000 359.17920 13.7% 41.5 5s
1083 706 390.32458 101 37 416.20000 362.24340 13.0% 33.7 10s
1099 717 399.43458 50 90 416.20000 362.24340 13.0% 33.2 15s
1945 833 cutoff 38 416.20000 364.76614 12.4% 35.9 20s
H 2880 1020 411.0000000 365.79614 11.0% 34.3 22s
4236 1785 400.01845 31 79 411.00000 376.77761 8.33% 33.7 25s
7139 3140 408.60763 100 105 411.00000 382.92742 6.83% 33.8 30s
9808 3821 407.68257 77 92 411.00000 387.47153 5.72% 34.9 35s
*10397 3819 34 409.7000000 388.20340 5.25% 34.9 35s
13496 3805 403.66281 34 62 409.70000 392.68727 4.15% 35.3 40s
16983 3258 cutoff 41 409.70000 396.55750 3.21% 35.1 45s
Cutting planes:
Gomory: 13
Cover: 32
Implied bound: 20
Projected implied bound: 1
Clique: 6
MIR: 7
StrongCG: 20
Flow cover: 40
Zero half: 55
Mod-K: 1
RLT: 129
Relax-and-lift: 3
Explored 23329 nodes (782255 simplex iterations) in 49.38 seconds
Thread count was 8 (of 8 available processors)
Solution count 8: 409.7 411 416.2 ... 491
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%MIPFocus=3 的情况留给读者朋友们自行测试。
Heuristics 参数的含义是我们在求解过程中花在启发式上的大致时间占比。

- 默认值=0.05,即约 5% 的算法使用启发式;
- > 0.05,意味着更激进地使用启发式,最大值为1;
- < 0.05,意味着更少地使用启式;
- =0 表示几乎不使用启发式。
我们首先取 Heuristics=0,即不使用数学启发式:
model = read("VRPTW_r102_20_5.mps")
model.setParam("Heuristics", 0)
model.optimize()求解日志如下: 发现设定后,除了找初始可行解以外,均无 H 标识,即未用到启发式算法。共使用了 49.27s 得到最优解。
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.03 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Changed value of parameter Heuristics to 0.0
Prev: 0.05 Min: 0.0 Max: 1.0 Default: 0.05
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.08s
Presolved: 1183 rows, 1519 columns, 16772 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Root relaxation: objective 2.871000e+02, 410 iterations, 0.02 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 37 - 287.10000 - - 0s
0 0 287.10000 0 59 - 287.10000 - - 0s
0 0 287.10000 0 64 - 287.10000 - - 0s
0 0 304.71668 0 83 - 304.71668 - - 0s
0 0 332.21792 0 82 - 332.21792 - - 0s
0 0 332.21792 0 85 - 332.21792 - - 0s
0 0 335.90452 0 80 - 335.90452 - - 0s
0 0 337.50589 0 95 - 337.50589 - - 0s
0 0 337.52434 0 92 - 337.52434 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 349.99973 0 105 - 349.99973 - - 0s
0 0 350.21622 0 108 - 350.21622 - - 0s
0 0 350.21622 0 108 - 350.21622 - - 0s
0 0 355.94000 0 114 - 355.94000 - - 0s
0 0 355.94000 0 114 - 355.94000 - - 0s
0 0 356.60000 0 73 - 356.60000 - - 0s
0 0 356.60000 0 98 - 356.60000 - - 0s
H 0 0 461.2000000 356.60000 22.7% - 1s
0 0 357.53333 0 61 461.20000 357.53333 22.5% - 1s
0 0 357.53333 0 59 461.20000 357.53333 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.77309 0 118 461.20000 357.77309 22.4% - 1s
0 0 357.77309 0 109 461.20000 357.77309 22.4% - 1s
0 2 357.77309 0 109 461.20000 357.77309 22.4% - 1s
1076 947 406.28774 23 94 461.20000 359.79903 22.0% 30.3 5s
1274 1080 407.78894 22 58 461.20000 366.62105 20.5% 36.5 10s
* 3113 1764 71 457.3000000 366.62105 19.8% 39.6 13s
* 4218 1924 51 433.5000000 366.62105 15.4% 38.0 14s
4796 2439 425.64721 141 79 433.50000 366.62105 15.4% 37.1 15s
9567 5481 403.75695 60 88 433.50000 374.55641 13.6% 40.1 20s
14170 8497 397.27875 42 59 433.50000 379.17515 12.5% 39.8 25s
*15815 5659 41 413.0000000 380.40000 7.89% 39.8 26s
18600 6429 406.02711 51 85 413.00000 383.27755 7.20% 40.7 30s
23597 7234 408.83624 32 58 413.00000 388.20832 6.00% 42.6 35s
*27133 6708 34 411.0000000 391.92714 4.64% 43.5 39s
27723 6637 cutoff 24 411.00000 392.70173 4.45% 43.6 40s
*28869 6136 46 409.7000000 393.43971 3.97% 43.9 41s
32747 4501 cutoff 27 409.70000 398.71111 2.68% 44.1 45s
Cutting planes:
Gomory: 11
Cover: 78
Implied bound: 37
Projected implied bound: 2
Clique: 5
MIR: 8
Flow cover: 32
Inf proof: 1
Zero half: 9
Mod-K: 4
RLT: 113
Relax-and-lift: 1
Explored 39241 nodes (1630810 simplex iterations) in 49.27 seconds
Thread count was 8 (of 8 available processors)
Solution count 6: 409.7 411 413 ... 461.2
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%接下来我们设 Heuristics=0.5:
model = read("VRPTW_r102_20_5.mps")
model.setParam("Heuristics", 0.5)
model.optimize()日志如下:使用了更多的启发式算法来得到可行解,一共耗时 108.29s。
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.03 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Changed value of parameter Heuristics to 0.5
Prev: 0.05 Min: 0.0 Max: 1.0 Default: 0.05
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.12s
Presolved: 1183 rows, 1519 columns, 16772 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Root relaxation: objective 2.871000e+02, 410 iterations, 0.02 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 37 - 287.10000 - - 0s
0 0 287.10000 0 59 - 287.10000 - - 0s
0 0 287.10000 0 64 - 287.10000 - - 0s
0 0 304.71668 0 83 - 304.71668 - - 0s
0 0 332.21792 0 82 - 332.21792 - - 0s
0 0 332.21792 0 85 - 332.21792 - - 0s
0 0 335.90452 0 80 - 335.90452 - - 0s
0 0 337.50589 0 95 - 337.50589 - - 0s
0 0 337.52434 0 92 - 337.52434 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 1s
0 0 343.62317 0 95 - 343.62317 - - 1s
0 0 349.99973 0 105 - 349.99973 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 356.60000 0 73 - 356.60000 - - 1s
0 0 356.60000 0 98 - 356.60000 - - 1s
0 0 357.53333 0 61 - 357.53333 - - 1s
0 0 357.53333 0 59 - 357.53333 - - 1s
0 0 357.63085 0 109 - 357.63085 - - 1s
0 0 357.63085 0 109 - 357.63085 - - 1s
0 0 357.77309 0 118 - 357.77309 - - 1s
H 0 0 461.2000000 357.77309 22.4% - 1s
0 0 357.77309 0 113 461.20000 357.77309 22.4% - 1s
0 2 357.81724 0 109 461.20000 357.81724 22.4% - 1s
H 31 40 448.7000000 357.95556 20.2% 74.5 2s
H 78 84 444.6000000 357.95556 19.5% 48.3 2s
H 156 150 419.4000000 357.95556 14.7% 38.9 2s
H 188 185 409.7000000 357.95556 12.6% 36.8 2s
550 504 382.67153 110 90 409.70000 357.95556 12.6% 27.2 5s
1100 939 401.13470 202 125 409.70000 362.69583 11.5% 26.3 10s
1252 973 infeasible 22 409.70000 363.41829 11.3% 34.9 15s
1457 1003 372.18694 31 97 409.70000 363.41829 11.3% 38.2 20s
2234 1186 380.16481 51 139 409.70000 363.41829 11.3% 40.5 25s
3120 1318 392.96082 79 113 409.70000 363.41829 11.3% 40.1 31s
3845 1374 371.02073 35 135 409.70000 363.43804 11.3% 40.6 35s
5898 2422 394.76560 102 121 409.70000 376.25829 8.16% 39.7 40s
6684 2718 397.01624 40 75 409.70000 381.15009 6.97% 40.2 47s
8035 3185 402.99344 57 71 409.70000 383.41584 6.42% 40.2 50s
8952 3490 394.50306 60 104 409.70000 385.03628 6.02% 40.8 55s
10880 3830 399.49653 25 81 409.70000 387.57519 5.40% 40.4 60s
12297 3984 397.11425 43 50 409.70000 389.35493 4.97% 40.3 65s
13535 3918 408.66372 44 63 409.70000 391.43134 4.46% 40.7 70s
13734 3887 398.17993 29 65 409.70000 391.78729 4.37% 40.7 78s
14449 3780 401.63961 48 80 409.70000 392.03954 4.31% 40.7 81s
16230 3688 cutoff 76 409.70000 394.33623 3.75% 40.8 85s
17675 3257 406.66117 45 45 409.70000 396.31795 3.27% 40.7 92s
19804 2023 cutoff 82 409.70000 399.16605 2.57% 40.5 96s
20635 1608 cutoff 76 409.70000 400.37732 2.28% 40.3 102s
22052 587 cutoff 49 409.70000 403.15964 1.60% 39.6 105s
Cutting planes:
Gomory: 14
Cover: 35
Implied bound: 18
Clique: 6
MIR: 11
StrongCG: 3
Flow cover: 32
Inf proof: 1
Zero half: 13
RLT: 123
Relax-and-lift: 8
Explored 23061 nodes (894681 simplex iterations) in 108.29 seconds
Thread count was 8 (of 8 available processors)
Solution count 5: 409.7 419.4 444.6 ... 461.2
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%
model.optimize()
model.optimize()最后我们设到最最大值 Heuristics=1:
model = read("VRPTW_r102_20_5.mps")
model.setParam("Heuristics", 1)
model.optimize()日志如下:求解过程中几乎都是靠以 H 标识的启发式算法得到的可行整数解,没有 * ,说明的确非常激进地使用了启发式算法。但是整个求解过程使用了 142.53s(2m 23s),是目前用时最久的,初始可行解求解得也慢和差。可见过于激进的启发式算法可能反而会降低求解效率。
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.02 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Changed value of parameter Heuristics to 1.0
Prev: 0.05 Min: 0.0 Max: 1.0 Default: 0.05
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.09s
Presolved: 1183 rows, 1519 columns, 16772 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Root relaxation: objective 2.871000e+02, 410 iterations, 0.02 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 37 - 287.10000 - - 0s
0 0 287.10000 0 59 - 287.10000 - - 0s
0 0 287.10000 0 64 - 287.10000 - - 0s
0 0 304.71668 0 83 - 304.71668 - - 0s
0 0 332.21792 0 82 - 332.21792 - - 0s
0 0 332.21792 0 85 - 332.21792 - - 0s
0 0 335.90452 0 80 - 335.90452 - - 0s
0 0 337.50589 0 95 - 337.50589 - - 0s
0 0 337.52434 0 92 - 337.52434 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 1s
0 0 349.99973 0 105 - 349.99973 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 356.60000 0 73 - 356.60000 - - 1s
0 0 356.60000 0 98 - 356.60000 - - 1s
0 0 357.53333 0 61 - 357.53333 - - 1s
0 0 357.53333 0 59 - 357.53333 - - 1s
0 0 357.63085 0 109 - 357.63085 - - 1s
0 0 357.63085 0 109 - 357.63085 - - 1s
0 0 357.77309 0 118 - 357.77309 - - 1s
0 0 357.77309 0 113 - 357.77309 - - 1s
H 0 0 728.3000000 357.81724 50.9% - 18s
0 2 357.81724 0 113 728.30000 357.81724 50.9% - 18s
H 35 40 686.2000000 358.10136 47.8% 53.7 18s
H 37 40 674.1000000 358.10136 46.9% 52.6 18s
H 67 72 652.9000000 358.10136 45.2% 56.1 18s
H 70 72 561.8000000 358.10136 36.3% 54.8 18s
H 99 102 533.0000000 358.10136 32.8% 48.3 19s
H 131 133 516.7000000 358.10136 30.7% 45.6 19s
H 132 133 478.4000000 358.10136 25.1% 45.3 19s
H 161 161 460.2000000 358.10136 22.2% 41.5 19s
196 183 366.05430 48 77 460.20000 358.10136 22.2% 38.8 20s
H 197 183 452.1000000 358.10136 20.8% 38.6 20s
H 233 213 444.3000000 358.10136 19.4% 38.2 20s
H 267 241 435.3000000 358.10136 17.7% 40.0 20s
H 276 235 418.2000000 358.10136 14.4% 40.6 20s
657 508 396.33508 132 86 418.20000 358.10136 14.4% 33.3 26s
939 707 377.47089 34 64 418.20000 361.31795 13.6% 32.6 30s
1059 758 362.42000 13 88 418.20000 362.42000 13.3% 35.0 35s
1295 846 364.11532 27 74 418.20000 362.42000 13.3% 39.2 40s
1455 897 367.50000 33 49 418.20000 362.42000 13.3% 39.5 45s
H 1456 858 416.9000000 362.42000 13.1% 39.5 45s
1683 912 373.13009 41 81 416.90000 362.42000 13.1% 39.4 50s
1993 987 366.69790 31 115 416.90000 363.36190 12.8% 40.1 55s
2216 1000 371.34337 40 117 416.90000 363.36190 12.8% 39.6 60s
2566 1158 393.18949 64 95 416.90000 363.36190 12.8% 39.4 65s
H 2802 1075 414.9000000 368.97514 11.1% 39.3 68s
3021 1064 397.10591 32 71 414.90000 368.97514 11.1% 39.7 70s
H 3426 1158 409.7000000 372.06969 9.18% 39.9 73s
3457 1241 395.30163 57 85 409.70000 372.76167 9.02% 40.0 75s
3927 1401 395.64859 24 82 409.70000 373.48030 8.84% 39.5 80s
4412 1537 384.50904 31 80 409.70000 375.44238 8.36% 39.4 86s
4695 1695 387.65449 27 55 409.70000 376.24611 8.17% 39.3 90s
5312 1940 394.03866 39 67 409.70000 378.70566 7.57% 39.5 95s
5799 2074 403.96750 61 62 409.70000 378.96330 7.50% 39.6 100s
6708 2194 403.39437 66 88 409.70000 380.76193 7.06% 39.7 105s
7445 2320 cutoff 75 409.70000 383.77400 6.33% 40.6 110s
8421 2386 cutoff 36 409.70000 385.97199 5.79% 40.7 115s
9416 2331 cutoff 57 409.70000 387.73420 5.36% 40.8 120s
10206 2259 cutoff 60 409.70000 389.86965 4.84% 41.3 125s
12214 1842 cutoff 39 409.70000 394.30935 3.76% 40.9 131s
13649 952 cutoff 65 409.70000 398.23380 2.80% 40.3 135s
15154 328 cutoff 31 409.70000 400.56210 2.23% 39.1 140s
Cutting planes:
Gomory: 6
Cover: 48
Implied bound: 31
Projected implied bound: 1
Clique: 5
MIR: 13
StrongCG: 2
Flow cover: 24
Inf proof: 1
Zero half: 4
Mod-K: 3
RLT: 107
Relax-and-lift: 10
Explored 15713 nodes (604416 simplex iterations) in 142.53 seconds
Thread count was 8 (of 8 available processors)
Solution count 10: 409.7 414.9 416.9 ... 516.7
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%通过该参数可以调整去目标启发式中要探索的节点数。请注意,这个启发式只在 MIP 问题的 Root 根节点使用,而且只在其他根启发式没有找到可行的解决方案时应用。

注意:应用这个启发式的代价很高,而且通常会产生质量很差的解。一般来说,只有在其他方法,包括用默认设置探索树,不能产生可行的解决方案时,才使用它。
model = read("VRPTW_r102_20_5.mps")
model.setParam("ZeroObjNodes",100)
model.optimize()求解过程如下,总耗时 38.45s:
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.02 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Changed value of parameter ZeroObjNodes to 100
Prev: -1 Min: -1 Max: 2000000000 Default: -1
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.07s
Presolved: 1183 rows, 1519 columns, 16772 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Root relaxation: objective 2.871000e+02, 410 iterations, 0.02 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 37 - 287.10000 - - 0s
0 0 287.10000 0 59 - 287.10000 - - 0s
0 0 287.10000 0 64 - 287.10000 - - 0s
0 0 304.71668 0 83 - 304.71668 - - 0s
0 0 332.21792 0 82 - 332.21792 - - 0s
0 0 332.21792 0 85 - 332.21792 - - 0s
0 0 335.90452 0 80 - 335.90452 - - 0s
0 0 337.50589 0 95 - 337.50589 - - 0s
0 0 337.52434 0 92 - 337.52434 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 349.99973 0 105 - 349.99973 - - 0s
0 0 350.21622 0 108 - 350.21622 - - 0s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 356.60000 0 73 - 356.60000 - - 1s
0 0 356.60000 0 98 - 356.60000 - - 1s
0 0 357.53333 0 61 - 357.53333 - - 1s
H 0 0 461.2000000 357.53333 22.5% - 1s
0 0 357.53333 0 59 461.20000 357.53333 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.77309 0 118 461.20000 357.77309 22.4% - 1s
0 0 357.77309 0 109 461.20000 357.77309 22.4% - 1s
0 2 357.81724 0 109 461.20000 357.81724 22.4% - 1s
H 33 40 453.1000000 358.10075 21.0% 51.6 1s
H 111 104 449.3000000 358.10075 20.3% 37.8 1s
H 111 104 448.4000000 358.10075 20.1% 37.8 1s
H 139 147 439.2000000 358.10075 18.5% 35.6 2s
H 185 185 429.5000000 358.10075 16.6% 31.2 2s
H 221 219 421.8000000 358.10075 15.1% 28.9 2s
H 409 350 418.4000000 358.10075 14.4% 28.7 2s
1055 770 402.87441 11 46 418.40000 361.05189 13.7% 28.4 5s
1084 791 365.45524 15 111 418.40000 365.45524 12.7% 31.6 10s
3379 1505 378.98296 49 120 418.40000 372.24037 11.0% 40.9 15s
6248 2708 391.75197 43 77 418.40000 378.91004 9.44% 42.0 20s
7949 3345 397.66128 55 80 418.40000 381.79796 8.75% 43.1 25s
*12715 4168 44 414.9000000 388.34862 6.40% 44.0 29s
12722 4277 cutoff 59 414.90000 388.36514 6.40% 44.0 30s
*12785 3950 44 412.3000000 388.36514 5.81% 44.1 30s
*13527 3546 57 409.7000000 389.04944 5.04% 44.3 31s
17011 2483 infeasible 58 409.70000 396.50284 3.22% 45.2 35s
Cutting planes:
Gomory: 8
Cover: 46
Implied bound: 25
Clique: 7
MIR: 14
StrongCG: 8
Flow cover: 45
Inf proof: 2
Zero half: 10
RLT: 121
Relax-and-lift: 7
Explored 21289 nodes (910378 simplex iterations) in 38.45 seconds
Thread count was 8 (of 8 available processors)
Solution count 10: 409.7 412.3 414.9 ... 453.1
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%这个参数定义了通过泵式缩减启发式的次数,与上面的去目标启发式很类似,在 Gurobi 求解中也是应用在根结点,用于快速找到整数可行解。

model = read("VRPTW_r102_20_5.mps")
model.setParam("PumpPasses",1000)
model.optimize()求解过程如下,总耗时 42.45s:
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.02 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Changed value of parameter PumpPasses to 100
Prev: -1 Min: -1 Max: 2000000000 Default: -1
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.07s
Presolved: 1183 rows, 1519 columns, 16772 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Root relaxation: objective 2.871000e+02, 410 iterations, 0.02 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 37 - 287.10000 - - 0s
0 0 287.10000 0 59 - 287.10000 - - 0s
0 0 287.10000 0 64 - 287.10000 - - 0s
0 0 304.71668 0 83 - 304.71668 - - 0s
0 0 332.21792 0 82 - 332.21792 - - 0s
0 0 332.21792 0 85 - 332.21792 - - 0s
0 0 335.90452 0 80 - 335.90452 - - 0s
0 0 337.50589 0 95 - 337.50589 - - 0s
0 0 337.52434 0 92 - 337.52434 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 349.99973 0 105 - 349.99973 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 356.60000 0 73 - 356.60000 - - 1s
0 0 356.60000 0 98 - 356.60000 - - 1s
0 0 357.53333 0 61 - 357.53333 - - 1s
H 0 0 461.2000000 357.53333 22.5% - 1s
0 0 357.53333 0 59 461.20000 357.53333 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.77309 0 118 461.20000 357.77309 22.4% - 1s
0 0 357.77309 0 109 461.20000 357.77309 22.4% - 1s
Feasibility pump: pass 1, min int violation 7.189, total elapsed time 2s
Feasibility pump: no solution found in 39 passes
0 2 357.81724 0 109 461.20000 357.81724 22.4% - 2s
H 33 40 453.1000000 358.10075 21.0% 51.6 2s
H 111 104 449.3000000 358.10075 20.3% 37.8 2s
H 111 104 448.4000000 358.10075 20.1% 37.8 2s
H 139 147 439.2000000 358.10075 18.5% 35.6 2s
H 184 178 428.1000000 358.10075 16.4% 31.2 3s
H 218 211 418.4000000 358.10075 14.4% 28.8 3s
1046 859 416.57254 57 109 418.40000 359.73731 14.0% 23.1 5s
1076 879 372.62523 70 111 418.40000 366.77494 12.3% 22.4 10s
2158 1153 373.89471 49 76 418.40000 366.77494 12.3% 35.0 15s
5089 2285 388.67922 49 70 418.40000 380.75357 9.00% 36.7 20s
7423 3191 403.96801 73 72 418.40000 384.30284 8.15% 38.0 25s
12711 4775 cutoff 49 418.40000 390.24377 6.73% 39.0 30s
*14186 4684 63 413.0000000 391.43259 5.22% 39.2 33s
15712 4743 402.70422 36 102 413.00000 393.72555 4.67% 39.5 35s
*17491 4308 87 411.0000000 395.39355 3.80% 39.7 37s
19955 3326 cutoff 45 411.00000 399.47069 2.81% 39.6 40s
*20477 2986 66 409.7000000 399.55950 2.48% 39.5 40s
Cutting planes:
Gomory: 9
Cover: 60
Implied bound: 26
Projected implied bound: 2
Clique: 6
MIR: 24
StrongCG: 1
Flow cover: 26
Inf proof: 1
Zero half: 6
Mod-K: 1
RLT: 112
Relax-and-lift: 4
Explored 24379 nodes (902690 simplex iterations) in 42.45 seconds
Thread count was 8 (of 8 available processors)
Solution count 10: 409.7 411 413 ... 461.2
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%通过这个参数可以调整 RINS 启发式的频率。增加 RINS 启发式的频率,可以将MIP搜索的重点从证明最优性转移到寻找良好的可行方案上。但建议在试验这个参数之前,先试试 MIPFocus、ImproveStartGap 或 ImproveStartTime 参数。

- 默认值=-1:自动选择;
- =0:关闭RINS;
- =n:在 MIP 搜索树的每 n 个节点应用 RINS。
我们先尝试 RINS=1000:
model = read("VRPTW_r102_20_5.mps")
model.setParam("RINS",1000)
model.optimize()求解过程日志如下,求解时间 37.96s:
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.02 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Changed value of parameter RINS to 1000
Prev: -1 Min: -1 Max: 2000000000 Default: -1
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.07s
Presolved: 1183 rows, 1519 columns, 16772 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Root relaxation: objective 2.871000e+02, 410 iterations, 0.02 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 37 - 287.10000 - - 0s
0 0 287.10000 0 59 - 287.10000 - - 0s
0 0 287.10000 0 64 - 287.10000 - - 0s
0 0 304.71668 0 83 - 304.71668 - - 0s
0 0 332.21792 0 82 - 332.21792 - - 0s
0 0 332.21792 0 85 - 332.21792 - - 0s
0 0 335.90452 0 80 - 335.90452 - - 0s
0 0 337.50589 0 95 - 337.50589 - - 0s
0 0 337.52434 0 92 - 337.52434 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 349.99973 0 105 - 349.99973 - - 0s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 356.60000 0 73 - 356.60000 - - 1s
0 0 356.60000 0 98 - 356.60000 - - 1s
0 0 357.53333 0 61 - 357.53333 - - 1s
H 0 0 461.2000000 357.53333 22.5% - 1s
0 0 357.53333 0 59 461.20000 357.53333 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.77309 0 118 461.20000 357.77309 22.4% - 1s
0 0 357.77309 0 109 461.20000 357.77309 22.4% - 1s
0 2 357.81724 0 109 461.20000 357.81724 22.4% - 1s
H 1 4 448.7000000 357.81724 20.3% 23.0 1s
H 67 72 439.0000000 358.10075 18.4% 43.0 1s
H 113 107 429.8000000 358.10075 16.7% 40.0 2s
H 138 145 425.7000000 358.10075 15.9% 37.0 2s
H 231 222 422.3000000 358.10075 15.2% 30.9 3s
H 453 366 409.7000000 358.10075 12.6% 28.1 3s
1034 782 399.49074 36 109 409.70000 360.27309 12.1% 27.6 5s
1065 803 394.38596 19 80 409.70000 367.57278 10.3% 26.8 10s
2171 945 400.26688 51 65 409.70000 367.57278 10.3% 41.4 15s
5365 1603 cutoff 56 409.70000 384.06741 6.26% 42.8 20s
9294 2714 406.93497 46 41 409.70000 390.00000 4.81% 42.0 25s
10773 2889 399.11126 53 45 409.70000 391.84389 4.36% 42.0 30s
15487 2118 406.12712 44 25 409.70000 397.51258 2.97% 41.8 35s
Cutting planes:
Gomory: 21
Cover: 44
Implied bound: 28
Projected implied bound: 1
Clique: 8
MIR: 12
StrongCG: 8
Flow cover: 34
Inf proof: 2
Zero half: 9
RLT: 140
Relax-and-lift: 8
Explored 19744 nodes (781978 simplex iterations) in 37.96 seconds
Thread count was 8 (of 8 available processors)
Solution count 7: 409.7 422.3 425.7 ... 461.2
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%最后我们再尝试关闭 RINS:
model = read("VRPTW_r102_20_5.mps")
model.setParam("RINS",0)
model.optimize()运行结果如下:发现对于这个测试用例,不打开 RINS 求解也是很快,仅用了 33.88s。
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.02 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Changed value of parameter RINS to 0
Prev: -1 Min: -1 Max: 2000000000 Default: -1
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.10s
Presolved: 1183 rows, 1519 columns, 16772 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Root relaxation: objective 2.871000e+02, 410 iterations, 0.02 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 37 - 287.10000 - - 0s
0 0 287.10000 0 59 - 287.10000 - - 0s
0 0 287.10000 0 64 - 287.10000 - - 0s
0 0 304.71668 0 83 - 304.71668 - - 0s
0 0 332.21792 0 82 - 332.21792 - - 0s
0 0 332.21792 0 85 - 332.21792 - - 0s
0 0 335.90452 0 80 - 335.90452 - - 0s
0 0 337.50589 0 95 - 337.50589 - - 0s
0 0 337.52434 0 92 - 337.52434 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 349.99973 0 105 - 349.99973 - - 0s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 356.60000 0 73 - 356.60000 - - 1s
0 0 356.60000 0 98 - 356.60000 - - 1s
0 0 357.53333 0 61 - 357.53333 - - 1s
H 0 0 461.2000000 357.53333 22.5% - 1s
0 0 357.53333 0 59 461.20000 357.53333 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.77309 0 118 461.20000 357.77309 22.4% - 1s
0 0 357.77309 0 113 461.20000 357.77309 22.4% - 1s
0 2 357.77309 0 113 461.20000 357.77309 22.4% - 1s
1043 894 434.74922 48 91 461.20000 358.53227 22.3% 30.3 5s
* 2333 1399 30 448.6000000 362.00467 19.3% 39.2 9s
2777 1612 388.80519 28 49 448.60000 363.84440 18.9% 40.5 10s
* 4063 2090 35 439.4000000 367.40997 16.4% 40.6 11s
5301 3072 421.37952 35 74 439.40000 370.94065 15.6% 39.9 15s
H 5966 3154 432.6000000 372.36928 13.9% 39.8 15s
* 8376 4775 45 432.0000000 377.74554 12.6% 40.3 18s
10011 5853 417.64539 41 71 432.00000 379.26612 12.2% 39.5 20s
*11395 3611 28 412.3000000 380.29818 7.76% 39.4 21s
*12097 3214 43 409.7000000 381.96807 6.77% 39.7 22s
14659 3598 infeasible 44 409.70000 386.99833 5.54% 40.4 25s
20021 3031 cutoff 42 409.70000 396.28047 3.28% 41.1 30s
Cutting planes:
Gomory: 11
Cover: 59
Implied bound: 30
Projected implied bound: 3
Clique: 9
MIR: 21
StrongCG: 2
Flow cover: 53
Zero half: 10
RLT: 132
Relax-and-lift: 2
Explored 25489 nodes (998017 simplex iterations) in 33.88 seconds
Thread count was 8 (of 8 available processors)
Solution count 7: 409.7 412.3 432 ... 461.2
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%限制基于MIP的启发式方法(如RINS)所探索的节点数量,可以和 RINS 等方法的参数组合使用。探索更多的节点可以产生更好的解,但通常需要更长的时间。

首先,我们尝试设置 SubMIPNodes=0,即不允许启发式方法探索节点:
model = read("VRPTW_r102_20_5.mps")
model.setParam("SubMIPNodes",0)
model.optimize()日志结果如下,总耗时 43.10s:
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.02 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Changed value of parameter SubMIPNodes to 0
Prev: 500 Min: 0 Max: 2000000000 Default: 500
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.07s
Presolved: 1183 rows, 1519 columns, 16772 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Root relaxation: objective 2.871000e+02, 410 iterations, 0.02 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 37 - 287.10000 - - 0s
0 0 287.10000 0 59 - 287.10000 - - 0s
0 0 287.10000 0 64 - 287.10000 - - 0s
0 0 304.71668 0 83 - 304.71668 - - 0s
0 0 332.21792 0 82 - 332.21792 - - 0s
0 0 332.21792 0 85 - 332.21792 - - 0s
0 0 335.90452 0 80 - 335.90452 - - 0s
0 0 337.50589 0 95 - 337.50589 - - 0s
0 0 337.52434 0 92 - 337.52434 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 349.99973 0 105 - 349.99973 - - 0s
0 0 350.21622 0 108 - 350.21622 - - 0s
0 0 350.21622 0 108 - 350.21622 - - 0s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 356.60000 0 73 - 356.60000 - - 1s
0 0 356.60000 0 98 - 356.60000 - - 1s
0 0 357.53333 0 61 - 357.53333 - - 1s
H 0 0 461.2000000 357.53333 22.5% - 1s
0 0 357.53333 0 59 461.20000 357.53333 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.77309 0 118 461.20000 357.77309 22.4% - 1s
0 0 357.77309 0 109 461.20000 357.77309 22.4% - 1s
0 2 357.81724 0 109 461.20000 357.81724 22.4% - 1s
H 74 79 448.7000000 358.10075 20.2% 42.6 1s
H 898 850 444.6000000 358.10815 19.5% 24.1 3s
H 989 863 440.5000000 359.60556 18.4% 23.9 3s
1046 906 402.21270 15 60 440.50000 359.60556 18.4% 24.1 5s
H 1050 863 427.9000000 359.60556 16.0% 24.0 5s
1262 929 360.69620 21 102 427.90000 360.69620 15.7% 30.3 10s
4088 1981 412.14870 70 53 427.90000 372.62951 12.9% 35.7 15s
7693 4214 cutoff 52 427.90000 379.51544 11.3% 36.3 20s
* 8925 4820 58 427.1000000 380.60382 10.9% 36.5 21s
12083 6605 426.21735 110 63 427.10000 384.14410 10.1% 37.1 25s
*16159 7079 85 417.3000000 387.30672 7.19% 37.7 29s
16746 7174 414.12607 62 44 417.30000 387.44791 7.15% 37.7 30s
H19527 6664 414.3000000 390.69481 5.70% 38.7 32s
21627 6915 407.88216 87 59 414.30000 393.59984 5.00% 39.3 35s
*23820 5727 65 411.0000000 395.47896 3.78% 39.5 37s
*24970 4965 98 409.7000000 396.60267 3.20% 39.6 38s
26937 3724 cutoff 59 409.70000 400.30203 2.29% 39.5 40s
Cutting planes:
Gomory: 9
Cover: 68
Implied bound: 28
Projected implied bound: 1
Clique: 5
MIR: 15
StrongCG: 1
Flow cover: 46
Inf proof: 1
Zero half: 10
Mod-K: 3
RLT: 103
Explored 32039 nodes (1192216 simplex iterations) in 43.10 seconds
Thread count was 8 (of 8 available processors)
Solution count 10: 409.7 411 414.3 ... 461.2
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%接下来我们尝试将该参数值调到最大:
model = read("VRPTW_r102_20_5.mps")
model.setParam("SubMIPNodes",2000000000)
model.optimize()运行结果如下,共 45.70s,性能上差异不大:
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.02 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Changed value of parameter SubMIPNodes to 2000000000
Prev: 500 Min: 0 Max: 2000000000 Default: 500
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.07s
Presolved: 1183 rows, 1519 columns, 16772 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Root relaxation: objective 2.871000e+02, 410 iterations, 0.02 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 37 - 287.10000 - - 0s
0 0 287.10000 0 59 - 287.10000 - - 0s
0 0 287.10000 0 64 - 287.10000 - - 0s
0 0 304.71668 0 83 - 304.71668 - - 0s
0 0 332.21792 0 82 - 332.21792 - - 0s
0 0 332.21792 0 85 - 332.21792 - - 0s
0 0 335.90452 0 80 - 335.90452 - - 0s
0 0 337.50589 0 95 - 337.50589 - - 0s
0 0 337.52434 0 92 - 337.52434 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 349.99973 0 105 - 349.99973 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 356.60000 0 73 - 356.60000 - - 1s
0 0 356.60000 0 98 - 356.60000 - - 1s
0 0 357.53333 0 61 - 357.53333 - - 1s
H 0 0 461.2000000 357.53333 22.5% - 1s
0 0 357.53333 0 59 461.20000 357.53333 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.63085 0 109 461.20000 357.63085 22.5% - 1s
0 0 357.77309 0 118 461.20000 357.77309 22.4% - 1s
0 0 357.77309 0 109 461.20000 357.77309 22.4% - 1s
0 2 357.81724 0 109 461.20000 357.81724 22.4% - 1s
H 33 40 453.1000000 358.10075 21.0% 51.6 1s
H 111 104 449.3000000 358.10075 20.3% 37.8 1s
H 111 104 448.4000000 358.10075 20.1% 37.8 1s
H 139 147 439.2000000 358.10075 18.5% 35.6 2s
H 184 186 429.5000000 358.10075 16.6% 31.2 2s
H 219 216 426.1000000 358.10075 16.0% 28.9 2s
H 313 300 418.4000000 358.10075 14.4% 24.4 2s
1087 824 400.46989 26 114 418.40000 360.47759 13.8% 25.7 5s
1110 839 381.55491 73 104 418.40000 370.16148 11.5% 25.1 10s
H 1223 843 409.7000000 370.16148 9.65% 32.2 12s
2508 1046 cutoff 32 409.70000 371.52360 9.32% 38.7 15s
5237 2287 infeasible 43 409.70000 380.85210 7.04% 39.4 20s
6871 2666 401.35740 41 65 409.70000 383.70824 6.34% 39.9 27s
9272 3429 cutoff 57 409.70000 386.66684 5.62% 39.7 30s
13584 4072 408.74545 60 49 409.70000 391.47194 4.45% 40.1 35s
17742 3670 infeasible 35 409.70000 395.82742 3.39% 40.2 40s
23102 997 cutoff 84 409.70000 401.95271 1.89% 39.3 45s
Cutting planes:
Gomory: 15
Cover: 61
Implied bound: 30
Projected implied bound: 1
Clique: 5
MIR: 19
Flow cover: 12
Inf proof: 1
Zero half: 6
Mod-K: 5
RLT: 116
Relax-and-lift: 2
Explored 25105 nodes (950444 simplex iterations) in 45.70 seconds
Thread count was 8 (of 8 available processors)
Solution count 9: 409.7 418.4 426.1 ... 461.2
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%下面的三个参数可以同时使用,都是控制节点松弛启发式(NoRel):
- MinRelNodes:最小松弛启发式(Minimum relaxation heuristic)
这个参数定义了在最小松弛启发式中要探索的节点数。请注意,这个启发式也只在 MIP 的根节点应用,而且只在其他根启发式没有找到可行的解决方案时才用。


- NoRelHeurTime:节点松弛启发式的运行时间
这个参数限制 NoRel 启发式花费的时间(秒)。这个启发式是在解决根松弛之前搜索高质量的可行方案。在根松弛特别昂贵的模型上,它可能相当有用。
注意这个参数将引入非确定性 —— 不同的运行可能采取不同的路径。使用 NoRelHeurWork 参数可以得到确定性的结果。
这个参数中使用的工作度量很难精确定义。一个单位大约对应于一秒钟,但这取决于机器、核心数,在某些情况下还取决于模型。可能需要进行试验,为你的模型找到一个好的参数设置。

下面我们设定了一组参数:
model=read("VRPTW_r102_20_5.mps")
model.setParam("MinRelNodes",100)
model.setParam("NoRelHeurTime",20)
model.setParam("NoRelHeurWork",20)
model.optimize()优化过程和结果如下,总耗时 59.33s,期间使用了 NoRel heuristic 节点松弛启发式:
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.02 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Changed value of parameter MinRelNodes to 100
Prev: -1 Min: -1 Max: 2000000000 Default: -1
Changed value of parameter NoRelHeurTime to 20.0
Prev: 0.0 Min: 0.0 Max: inf Default: 0.0
Changed value of parameter NoRelHeurWork to 20.0
Prev: 0.0 Min: 0.0 Max: inf Default: 0.0
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.09s
Presolved: 1183 rows, 1519 columns, 16772 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Starting NoRel heuristic
Found phase-1 solution: relaxation 116.2
Found phase-1 solution: relaxation 107.5
Found phase-1 solution: relaxation 104.5
Found phase-1 solution: relaxation 14
Found phase-1 solution: relaxation 11
Found phase-1 solution: relaxation 8
Found phase-1 solution: relaxation 7
Found phase-1 solution: relaxation 6
Found phase-1 solution: relaxation 4
Found phase-1 solution: relaxation 2
Found phase-1 solution: relaxation 1
Found phase-1 solution: relaxation 2.84217e-14
Found heuristic solution: objective 596.5000000
Transition to phase 2
Found heuristic solution: objective 590.6000000
Found heuristic solution: objective 583.2000000
Found heuristic solution: objective 577.3000000
Found heuristic solution: objective 571.1000000
Found heuristic solution: objective 554.1000000
Found heuristic solution: objective 547.9000000
Found heuristic solution: objective 515.3000000
Found heuristic solution: objective 497.0000000
Found heuristic solution: objective 481.6000000
Found heuristic solution: objective 451.3000000
Found heuristic solution: objective 441.6000000
Found heuristic solution: objective 439.1000000
Found heuristic solution: objective 426.9000000
Found heuristic solution: objective 418.5000000
Elapsed time for NoRel heuristic: 5s (best bound 287.1)
Found heuristic solution: objective 418.3000000
Elapsed time for NoRel heuristic: 11s (best bound 287.1)
Found heuristic solution: objective 411.7000000
Elapsed time for NoRel heuristic: 17s (best bound 287.1)
Root simplex log...
Iteration Objective Primal Inf. Dual Inf. Time
0 0.0000000e+00 5.900000e+01 0.000000e+00 21s
410 2.8710000e+02 0.000000e+00 0.000000e+00 21s
Root relaxation: objective 2.871000e+02, 410 iterations, 0.03 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 37 411.70000 287.10000 30.3% - 20s
0 0 287.10000 0 59 411.70000 287.10000 30.3% - 20s
0 0 287.10000 0 58 411.70000 287.10000 30.3% - 20s
0 0 315.46053 0 64 411.70000 315.46053 23.4% - 20s
0 0 317.00000 0 53 411.70000 317.00000 23.0% - 20s
0 0 325.07451 0 100 411.70000 325.07451 21.0% - 20s
0 0 339.58000 0 97 411.70000 339.58000 17.5% - 21s
0 0 339.58000 0 87 411.70000 339.58000 17.5% - 21s
0 0 342.81925 0 111 411.70000 342.81925 16.7% - 21s
0 0 344.46400 0 104 411.70000 344.46400 16.3% - 21s
0 0 344.46400 0 97 411.70000 344.46400 16.3% - 21s
0 0 352.13492 0 100 411.70000 352.13492 14.5% - 21s
0 0 352.27994 0 100 411.70000 352.27994 14.4% - 21s
0 0 352.27994 0 100 411.70000 352.27994 14.4% - 21s
0 0 354.80909 0 99 411.70000 354.80909 13.8% - 21s
0 0 355.23303 0 103 411.70000 355.23303 13.7% - 21s
0 0 355.24175 0 106 411.70000 355.24175 13.7% - 21s
0 0 356.73412 0 97 411.70000 356.73412 13.4% - 21s
0 0 356.79709 0 109 411.70000 356.79709 13.3% - 21s
0 0 356.79709 0 109 411.70000 356.79709 13.3% - 21s
0 0 357.20248 0 122 411.70000 357.20248 13.2% - 21s
0 0 357.31707 0 130 411.70000 357.31707 13.2% - 21s
0 0 357.45069 0 120 411.70000 357.45069 13.2% - 21s
0 0 357.45069 0 120 411.70000 357.45069 13.2% - 21s
0 0 357.45069 0 124 411.70000 357.45069 13.2% - 21s
0 0 357.45069 0 124 411.70000 357.45069 13.2% - 21s
0 0 357.45208 0 114 411.70000 357.45208 13.2% - 21s
0 0 357.45208 0 114 411.70000 357.45208 13.2% - 21s
0 2 357.53094 0 114 411.70000 357.53094 13.2% - 22s
996 850 393.99451 56 83 411.70000 358.72773 12.9% 33.1 25s
1077 869 384.57811 71 92 411.70000 365.42688 11.2% 31.9 30s
1108 890 378.57357 16 95 411.70000 374.50583 9.03% 31.0 35s
1145 916 392.24865 10 158 411.70000 375.82925 8.71% 33.6 40s
1883 1039 377.28568 48 77 411.70000 375.82925 8.71% 38.2 45s
4923 1657 401.80816 57 90 411.70000 387.69237 5.83% 39.6 50s
8030 1994 infeasible 80 411.70000 393.80687 4.35% 39.6 55s
* 8350 1944 67 409.7000000 394.03437 3.82% 39.5 55s
Cutting planes:
Gomory: 14
Cover: 28
Implied bound: 16
Projected implied bound: 3
Clique: 3
MIR: 9
StrongCG: 8
Flow cover: 46
Zero half: 17
RLT: 114
Relax-and-lift: 4
Explored 12710 nodes (468602 simplex iterations) in 59.33 seconds
Thread count was 8 (of 8 available processors)
Solution count 10: 409.7 411.7 418.3 ... 497
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%MIP 求解器可以在搜索过程中改变参数设置,以便采用一种放弃移动最佳边界的策略,而将全部精力用于寻找更好的可行方案。有以下三个参数可以进行设置:
- ImproveStartGap
这个参数允许你指定一个优化 gap%,当求解过程达到了这个 gap% 上,MIP 求解器会切换到一个改进策略。例如,将此参数设置为 0.1 将导致 MIP 求解器在相对最优性差距小于 10% 时切换策略。


- ImproveStartNodes
这个参数允许你指定 MIP 求解器切换到改进策略的节点数。例如,将此参数设置为 10 将导致MIP求解器在节点数大于 10 时切换策略。

- ImproveStartTime
这个参数允许你指定 MIP 求解器切换改进策略的时间。例如,将此参数设置为10将导致MIP求解器在开始优化后 10 秒内切换策略。

下面我们设定了一组参数:
model=read("VRPTW_r102_20_5.mps")
model.setParam("ImproveStartGap",10)
model.setParam("ImproveStartNodes",3000)
model.setParam("ImproveStartTime",20)
model.optimize()优化过程和结果如下,期间自动使用了(Heuristics=0.5 and RINS=10) 优化参数。但发现求解速度非常慢,总耗时达到 927.98s(15m 28s):
Read MPS format model from file VRPTW_r102_20_5.mps
Reading time=0.02 seconds
VRPTW: 1797 rows, 1525 columns, 14416 nonzeros
Changed value of parameter ImproveStartGap to 10.0
Prev: 0.0 Min: 0.0 Max: inf Default: 0.0
Changed value of parameter ImproveStartNodes to 3000.0
Prev: inf Min: 0.0 Max: inf Default: inf
Changed value of parameter ImproveStartTime to 20.0
Prev: inf Min: 0.0 Max: inf Default: inf
Gurobi Optimizer version 9.1.0 build v9.1.0rc0 (win64)
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1797 rows, 1525 columns and 14416 nonzeros
Model fingerprint: 0x4a4bba28
Variable types: 110 continuous, 1415 integer (1415 binary)
Coefficient statistics:
Matrix range[1e+00, 3e+02]
Objective range[7e+00, 6e+01]
Bounds range[1e+00, 2e+02]
RHS range[1e+00, 3e+02]
Presolve removed 614 rows and 6 columns
Presolve time: 0.09s
Presolved: 1183 rows, 1519 columns, 16772 nonzeros
Variable types: 100 continuous, 1419 integer (1415 binary)
Root relaxation: objective 2.871000e+02, 410 iterations, 0.02 seconds
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 287.10000 0 37 - 287.10000 - - 0s
0 0 287.10000 0 59 - 287.10000 - - 0s
0 0 287.10000 0 64 - 287.10000 - - 0s
0 0 304.71668 0 83 - 304.71668 - - 0s
0 0 332.21792 0 82 - 332.21792 - - 0s
0 0 332.21792 0 85 - 332.21792 - - 0s
0 0 335.90452 0 80 - 335.90452 - - 0s
0 0 337.50589 0 95 - 337.50589 - - 0s
0 0 337.52434 0 92 - 337.52434 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 343.62317 0 95 - 343.62317 - - 0s
0 0 349.99973 0 105 - 349.99973 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 350.21622 0 108 - 350.21622 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 355.94000 0 114 - 355.94000 - - 1s
0 0 356.60000 0 73 - 356.60000 - - 1s
0 0 356.60000 0 98 - 356.60000 - - 1s
0 0 357.53333 0 61 - 357.53333 - - 1s
H 0 0 461.2000000 357.53333 22.5% - 1s
0 0 357.53333 0 59 461.20000 357.53333 22.5% - 1s
Resetting heuristic parameters to focus on improving solution
(using Heuristics=0.5 and RINS=10)...
H 3 4 451.5000000 357.85000 20.7% 81.3 1s
H 11 12 439.0000000 357.85000 18.5% 120 2s
H 13 14 422.3000000 357.85000 15.3% 108 2s
H 16 17 409.7000000 357.85000 12.7% 98.1 2s
72 15 403.86858 12 56 409.70000 357.85000 12.7% 52.4 5s
115 18 cutoff 17 409.70000 357.85000 12.7% 45.7 10s
183 30 370.10000 7 50 409.70000 358.05909 12.6% 47.0 15s
225 41 405.26226 10 54 409.70000 358.31765 12.5% 46.0 20s
285 55 395.63333 14 20 409.70000 358.31765 12.5% 42.8 25s
368 77 399.61273 27 16 409.70000 358.31765 12.5% 40.8 30s
431 100 cutoff 17 409.70000 358.83333 12.4% 42.9 35s
485 111 cutoff 21 409.70000 358.83333 12.4% 42.2 40s
561 125 404.95689 34 59 409.70000 358.83333 12.4% 41.7 45s
634 141 400.04932 16 67 409.70000 359.25000 12.3% 42.9 50s
725 166 395.39709 21 62 409.70000 359.25000 12.3% 42.6 56s
771 186 398.97650 25 32 409.70000 359.33028 12.3% 43.6 60s
863 203 401.00927 20 55 409.70000 359.33028 12.3% 42.4 66s
922 225 402.04470 26 51 409.70000 359.33028 12.3% 41.7 71s
1049 253 369.42982 18 65 409.70000 360.78033 11.9% 41.3 75s
1102 269 cutoff 23 409.70000 360.78033 11.9% 42.3 80s
1209 298 385.94144 20 87 409.70000 360.78033 11.9% 42.5 86s
1311 326 388.07853 26 87 409.70000 360.78033 11.9% 42.9 91s
1407 354 cutoff 38 409.70000 361.07619 11.9% 43.0 97s
1462 370 394.09537 25 70 409.70000 361.44811 11.8% 42.6 100s
1610 413 362.05714 25 98 409.70000 362.00000 11.6% 43.6 107s
1681 433 376.14483 28 88 409.70000 362.00000 11.6% 44.0 110s
1806 459 cutoff 29 409.70000 362.05714 11.6% 43.7 116s
1854 463 cutoff 30 409.70000 362.50294 11.5% 43.7 120s
1984 508 385.38974 33 80 409.70000 363.55625 11.3% 43.4 128s
2073 519 387.51076 37 67 409.70000 363.55625 11.3% 43.6 133s
2138 553 369.24570 41 105 409.70000 363.55625 11.3% 43.5 137s
2230 573 infeasible 56 409.70000 363.81359 11.2% 43.5 142s
2318 595 393.37500 30 57 409.70000 364.58075 11.0% 43.4 147s
2426 626 infeasible 34 409.70000 364.74286 11.0% 42.9 152s
2575 641 401.32573 49 64 409.70000 365.06944 10.9% 42.5 157s
2682 665 infeasible 47 409.70000 365.85000 10.7% 42.5 163s
2737 688 cutoff 50 409.70000 367.94375 10.2% 42.8 169s
2854 706 403.12941 57 41 409.70000 369.75903 9.75% 42.5 176s
2959 730 cutoff 55 409.70000 369.75903 9.75% 42.2 182s
3122 742 396.97684 9 99 409.70000 369.77009 9.75% 41.7 186s
3186 754 369.77009 17 114 409.70000 369.77009 9.75% 42.9 191s
3230 743 406.01299 18 75 409.70000 369.77009 9.75% 43.1 196s
3257 734 384.27257 18 88 409.70000 369.77009 9.75% 43.1 200s
3288 735 369.77009 18 67 409.70000 369.77009 9.75% 43.2 205s
3354 719 403.40475 21 40 409.70000 369.77009 9.75% 43.5 211s
3412 719 394.89398 26 99 409.70000 369.77009 9.75% 43.5 216s
3492 710 405.60354 29 32 409.70000 369.77009 9.75% 43.5 221s
3532 709 400.94094 28 70 409.70000 369.77009 9.75% 43.5 225s
3587 708 369.77009 19 78 409.70000 369.77009 9.75% 43.9 230s
3660 693 407.73068 21 47 409.70000 369.77009 9.75% 44.3 236s
3795 673 375.38056 23 72 409.70000 369.77009 9.75% 44.7 242s
3896 668 cutoff 27 409.70000 369.77009 9.75% 44.8 246s
4004 655 369.77009 25 88 409.70000 369.77009 9.75% 45.0 251s
4082 661 403.98528 27 26 409.70000 369.77009 9.75% 44.6 255s
4256 632 398.97533 30 87 409.70000 369.77009 9.75% 44.9 261s
4362 616 cutoff 38 409.70000 369.77009 9.75% 45.1 266s
4427 600 405.50000 41 42 409.70000 369.77009 9.75% 45.1 271s
4474 595 393.22879 28 92 409.70000 369.77009 9.75% 45.1 278s
4501 617 388.20651 29 94 409.70000 369.77009 9.75% 45.3 281s
4573 606 infeasible 31 409.70000 369.77009 9.75% 45.3 285s
4723 577 377.09549 32 67 409.70000 369.77009 9.75% 45.3 292s
4844 552 403.02258 36 57 409.70000 369.77009 9.75% 45.4 295s
5043 511 405.84995 39 85 409.70000 369.77009 9.75% 45.6 303s
5125 507 infeasible 43 409.70000 369.77009 9.75% 45.5 307s
5225 478 388.63598 36 84 409.70000 369.77009 9.75% 45.5 311s
5299 488 393.59892 40 85 409.70000 369.77009 9.75% 45.5 316s
5461 497 400.11808 49 86 409.70000 371.62716 9.29% 45.4 320s
5524 525 cutoff 37 409.70000 371.62716 9.29% 45.4 325s
5666 551 408.18806 43 67 409.70000 371.92051 9.22% 45.2 330s
5864 557 372.68492 41 120 409.70000 372.68492 9.03% 44.8 335s
5951 577 387.19397 45 67 409.70000 373.35000 8.87% 44.7 340s
6080 609 376.01202 43 121 409.70000 373.35276 8.87% 44.9 346s
6242 624 375.11823 45 92 409.70000 373.43916 8.85% 44.7 351s
6344 639 382.82587 47 83 409.70000 373.43916 8.85% 44.7 357s
6408 651 399.18985 50 64 409.70000 373.43916 8.85% 44.7 363s
6488 688 cutoff 38 409.70000 375.16429 8.43% 44.6 369s
6781 711 cutoff 33 409.70000 376.91290 8.00% 44.5 376s
6883 746 cutoff 39 409.70000 377.06604 7.97% 44.4 382s
7096 792 cutoff 49 409.70000 377.98056 7.74% 44.3 389s
7268 808 397.12805 60 79 409.70000 377.98056 7.74% 44.6 396s
7399 853 405.60375 66 38 409.70000 378.46479 7.62% 44.4 403s
7717 903 cutoff 31 409.70000 381.70042 6.83% 44.4 411s
7939 915 403.80535 58 62 409.70000 381.70042 6.83% 44.3 418s
8052 942 cutoff 54 409.70000 382.50000 6.64% 44.2 425s
8302 966 408.66035 45 86 409.70000 383.28690 6.45% 44.1 432s
8499 971 cutoff 42 409.70000 383.58408 6.37% 43.8 442s
8569 980 404.98586 31 44 409.70000 383.68867 6.35% 43.7 451s
8645 1013 infeasible 42 409.70000 383.70452 6.35% 43.6 460s
8897 1054 404.33574 50 48 409.70000 384.10492 6.25% 43.4 469s
9265 1074 cutoff 38 409.70000 384.41366 6.17% 43.2 479s
9407 1117 cutoff 47 409.70000 384.59646 6.13% 43.1 488s
9832 1148 407.79126 49 59 409.70000 385.17092 5.99% 42.9 497s
10139 1136 cutoff 68 409.70000 385.17092 5.99% 42.8 509s
10213 1143 406.19803 70 15 409.70000 385.85841 5.82% 42.7 521s
10316 1159 404.49828 45 72 409.70000 386.05906 5.77% 42.6 533s
10527 1282 389.05903 39 69 409.70000 386.32635 5.71% 42.4 544s
11666 1297 397.40000 32 12 409.70000 387.58226 5.40% 41.8 556s
11875 1344 404.22375 39 27 409.70000 387.62428 5.39% 41.7 569s
12348 1377 infeasible 62 409.70000 388.21450 5.24% 41.5 583s
12671 1418 cutoff 63 409.70000 388.65865 5.14% 41.4 598s
13323 1421 cutoff 50 409.70000 389.18927 5.01% 41.1 612s
13535 1429 cutoff 73 409.70000 389.44522 4.94% 41.0 626s
14075 1440 408.02361 53 52 409.70000 389.96418 4.82% 40.6 641s
14760 1445 infeasible 51 409.70000 390.52994 4.68% 40.3 658s
15048 1480 393.09352 49 84 409.70000 390.78619 4.62% 40.2 673s
15782 1441 400.17823 69 55 409.70000 391.40548 4.47% 40.0 691s
17451 1441 cutoff 59 409.70000 392.98809 4.08% 39.4 700s
17555 1469 cutoff 69 409.70000 393.08502 4.06% 39.3 708s
17745 1468 406.23138 84 68 409.70000 393.32683 4.00% 39.3 717s
18022 1428 403.46050 82 74 409.70000 393.67349 3.91% 39.2 726s
18699 1422 cutoff 46 409.70000 394.61712 3.68% 39.0 736s
19028 1413 cutoff 74 409.70000 394.88860 3.62% 38.9 748s
19176 1373 cutoff 56 409.70000 395.23349 3.53% 38.8 760s
19706 1379 397.71322 53 97 409.70000 395.76344 3.40% 38.6 773s
19956 1333 401.78059 44 62 409.70000 396.06190 3.33% 38.5 788s
20403 1233 cutoff 31 409.70000 396.53459 3.21% 38.4 802s
21303 1238 cutoff 34 409.70000 397.22974 3.04% 38.0 818s
21737 1162 cutoff 35 409.70000 397.76137 2.91% 37.8 831s
22665 1115 404.35087 94 55 409.70000 398.94333 2.63% 37.4 847s
23044 1050 402.33474 54 57 409.70000 399.35104 2.53% 37.3 864s
23481 950 404.74992 59 73 409.70000 400.09686 2.34% 37.1 883s
24153 618 cutoff 91 409.70000 400.81197 2.17% 36.7 902s
25535 307 infeasible 86 409.70000 403.33417 1.55% 35.7 918s
26276 0 cutoff 54 409.70000 405.20001 1.10% 35.2 927s
Cutting planes:
Gomory: 10
Cover: 23
Implied bound: 54
Clique: 9
MIR: 13
StrongCG: 6
Flow cover: 39
Inf proof: 5
Zero half: 16
RLT: 150
Relax-and-lift: 11
Explored 26748 nodes (932512 simplex iterations) in 927.98 seconds
Thread count was 8 (of 8 available processors)
Solution count 5: 409.7 422.3 439 ... 461.2
Optimal solution found (tolerance 1.00e-04)
Best objective 4.097000000000e+02, best bound 4.097000000000e+02, gap 0.0000%我们将以上测试结果进行汇总,如下表所示。可知各个启发式算法的参数设置对求解结果的影响有时候是很大的,以及,并没有明确的证据表明,在特定的参数下,求解效果就一定好。因此需要用户自行进行调优和测试,具体问题具体分析。
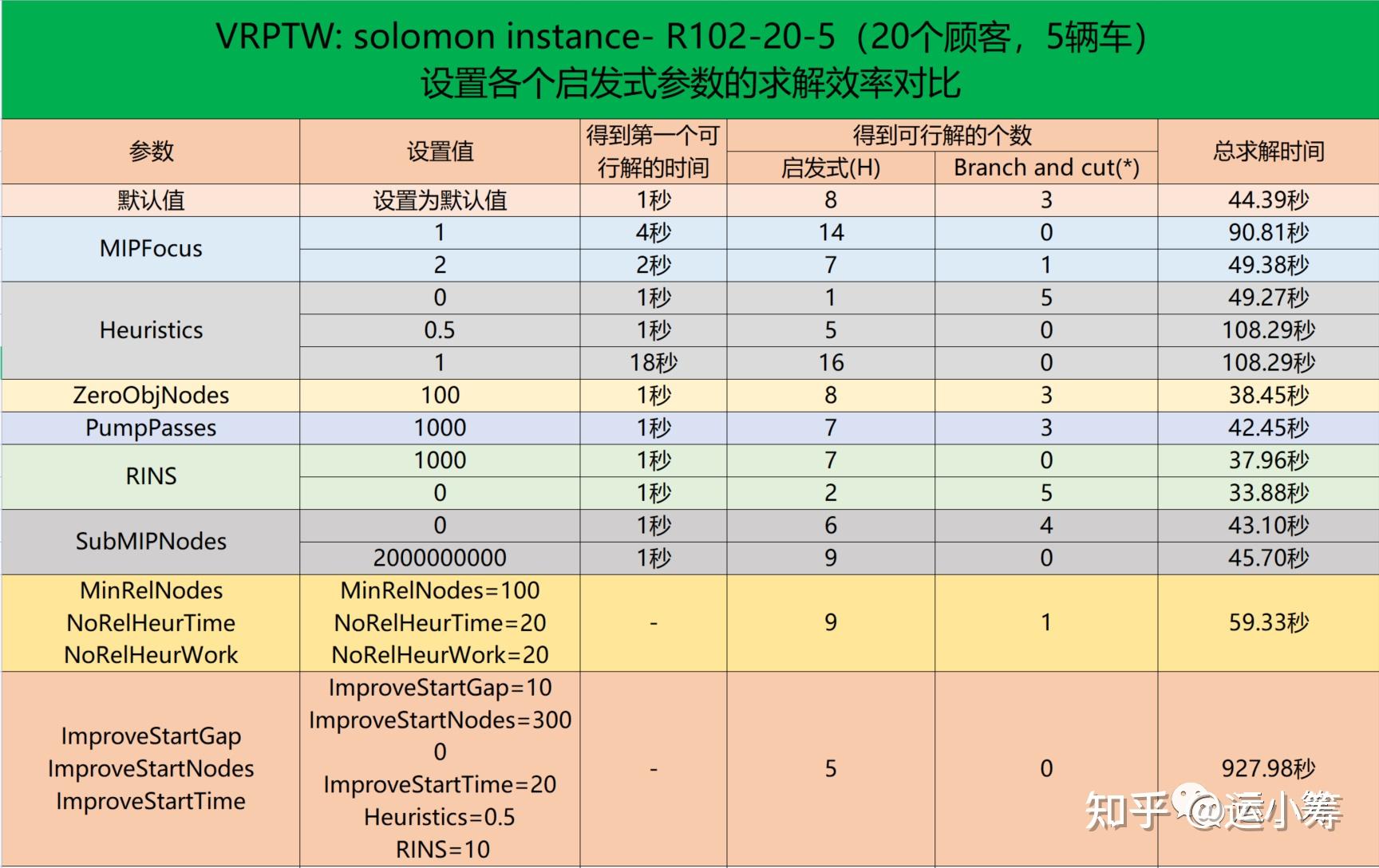
以上就是本文的全部内容,在本文中,我们首先介绍了什么是数学启发式 Matheuristics,然后分类介绍了 Gurobi 求解器里提供的启发式算法类别以及大致思想,并列举了涉及到的重要参数。在最后的案例实验中,我们依次添加了各类参数,并通过日志分别查看参数对求解性能的影响。但正如天下没有免费的午餐,启发式其实未必总能提高效率,在实际应用中,依然需要使用者对研究的问题领域以及每类启发式算法的原理有足够的理解才能用好这些工具。希望本文的内容能够对大家使用数学启发式有所帮助。
280页运小筹优化理论教程发布(2022年3月--2022年6月)
可以从下方链接详细阅览:
重磅硬货!280页运小筹优化理论教程发布(2022年3月--2022年6月)!

关注我们运小筹公众号
运小筹公众号致力于分享运筹优化(LP、MIP、NLP、随机规划、鲁棒优化)、凸优化、强化学习等研究领域的内容以及涉及到的算法的代码实现。编程语言和工具包括Java、Python、Matlab、CPLEX、Gurobi、SCIP 等。欢迎广大同行投稿!欢迎大家关注我们的公众号“运小筹”以及粉丝群!
如果群满加不进去,可以加本文作者微信,然后备注姓名+机构+专业,然后拉您入群。
第114篇:重磅硬货!280页运小筹优化理论教程发布(2022年3月--2022年6月)!
第113篇:优化 | 分支定界算法案例实战:Python调用COPT实现
第112篇:优化 | 分支定界算法案例实战:Python调用COPT实现
第111篇:优化 | 五个经典设施选址模型的详解及其实践:Python调用Gurobi实现
第110篇:始于初心,回馈教育:运筹与智能决策教学平台——杉数CORIDM全新升级上线!
第109篇:求解器COPT实践详解丨数学规划视角下的分货优化解题思路
第108篇:论文代码复现 | 考虑客户位置移动的车辆路径规划问题:MIP模型详解及Java调用CPLEX求解的完整代码
第107篇:求解器COPT实践丨地铁乘务排班问题如何优化求解
第106篇:优化求解器 | 求解器加速的高级技能包:MIP模型初始解设置相关操作的超详细解读
第105篇:OR Talk Pool:【8月26日-9月3日】近期讲座、课程和研讨会
第104篇:OR Talk Pool:【8月17日-8月31日】近期研讨会、论坛和培训
第103篇:进展 | 清华大学SIGS戚铭尧及其合作者在顶级期刊Operations Research上发表竞争性设施选址问题的最新研究进展
第102篇:启发式算法和优化算法设计及调试技巧 | AIRS in the AIR“运筹优化”系列讲座
第101篇:OR Talk Pool【8月9日-8月31号】:近期研讨会、论坛和培训
第100篇:理论算法与精确算法 | AIRS in the AIR”运筹优化“系列讲座
第99篇:OR Talk Pool【7月27日-8月】:近期研讨会、论坛和培训
第98篇:优化求解器|Solution Pool用法的超详细解读(Gurobi):最优解与多个可行解的获取与分析(案例与代码实现)
第96篇:OR Talk Pool【7月6日-7月13日】:近期研讨会、论坛和培训
第94篇:优化 | 手把手教你用C++调用Gurobi求解CVRP:环境配置、数学模型及完整代码
第93篇:OR Talk Pool:近期研讨会、暑期学校和学术报告推荐
第92篇:优化求解器 | Gurobi的MVar类:矩阵建模利器、求解对偶问题的备选方案 (附详细案例+代码)
第91篇:【求解器】Gurobi中非线性约束的对偶值的获取:QCP、QCQP、SOCP | 以及求解器最优性理论证明
第90篇:优化 | 二部图最大匹配问题的精确算法详解(HK算法和匈牙利算法):一份让您满意的【理论介绍+代码实现】学习笔记
第89篇:优化算法 | Benders Decomposition: 一份让你满意的【入门-编程实战-深入理解】的学习笔记
第88篇:优化 | 史上最【皮】数学题求解的新尝试:一种求解器的视角 (Python调用Gurobi实现)
第87篇:优化 | 寻找新的建模视角——从直观解释对偶问题入手:以Cutting Stock Problem的对偶问题为例
第86篇:ORers‘ Bling Chat【03】 | 【高光聊天记录集锦】:运小筹读者群里那些热烈的讨论
第85篇:非线性优化 | 非线性问题线性化以及求解的详细案例及Python+Gurobi求解
第84篇:ORers' Bling Chat | 【高光聊天记录集锦-02】:运小筹读者群里那些热烈的讨论
第83篇:Machine-Learning–Based Column Selection for Column Generation
第82篇:最新!205页运小筹优化理论学习笔记发布(2021年9月--2022年3月)!
第81篇:【鲁棒优化】| 补充证明:为什么最优解一定满足取值等于绝对值(论文笔记:The Price of Robustness)
第80篇:【鲁棒优化】| 论文笔记:The Price of Robustness - 列不确定性模型部分的推导和一些思考
第79篇:ORers' Bling Chat | 【高光聊天记录集锦-01】:运小筹读者群里那些热烈的讨论
第78篇:优化| 手把手教你学会杉数求解器(COPT)的安装、配置与测试
第77篇:【教学视频】优化 | 线性化(2):连续变量 * 0-1变量的线性化
第76篇:【教学视频】优化 | 线性化:两个0-1变量相乘的线性化
第75篇:强化学习实战 | DQN和Double DQN保姆级教程:以Cart-Pole为例
第74篇:强化学习| 概念梳理:强化学习、马尔科夫决策过程与动态规划
第73篇:强化学习实战 | Q-learning求解最短路(SPP)问题
第72篇:鲁棒优化 | 以Coding入门鲁棒优化:以一个例子引入(二)
第71篇:鲁棒优化|基于ROME编程入门鲁棒优化:以一个例子引入(一)
第70篇:优化|含分式的非线性规划求解: 基于Outer Approximation的Branch-and-cut 算法及其Java实现
第69篇:科研工具 | 手把手教你玩转文献管理神器:Endnote
第68篇:相约深圳 | 2022 INFORMS 服务科学国际会议·征稿通知
第67篇:鲁棒优化| 利用rome求解鲁棒优化简单案例:以CVaR不确定性集为例
第65篇:最新!145页运小筹优化理论学习笔记发布(2021年4月--9月)!
第64篇:优化 | 手把手教你用Python调用SCIP求解最优化模型
第63篇:优化 | 随机规划案例:The value of the stochastic solution
第62篇:工具 | draw.io: 科研流程示意图必备大杀器
第61篇:优化 | 开源求解器SCIP的安装与入门教程(Windows+Python)
第60篇:优化|Gurobi处理非线性目标函数和约束的详细案例
第58篇:测试算例下载:《运筹优化常用模型、算法及案例实战:代码手册》
第57篇:鲁棒优化|分布式鲁棒优化转化为SOCP案例及代码实现(Python+RSOME)
第56篇:鲁棒优化 | 分布式鲁棒优化简单案例及实战(RSOME+Gurobi)
第55篇:【尾款+发货】|【代码手册】 《运筹优化常用模型、算法及案例实战:Python+Java
第52篇:【视频讲解】CPLEX的OPL语言:可视化的优化模型求解解决方案
第51篇:算法 | 基于英雄联盟寻路背景的A星算法及python实现
第50篇:【转发】清华大学深圳国际研究生院2021年物流工程与管理项目优秀大学生夏令营报名通知
第49篇:优化 | 精确算法之分支定界介绍和实现(附Python代码)
第47篇:【重新发布】|《运筹优化常用模型、算法及案例实战:Python+Java实现》 【代码手册】 开始预购啦!!!
第46篇:智慧交通可视化:手把手教你用Python做出行数据可视化-osmnx 包入门教程
第45篇:优化 | Pick and delivery problem的介绍与建模实现(二)
第43篇:元启发式算法 | 遗传算法(GA)解决TSP问题(Python实现)
第42篇:优化|视频详解Python调用Gurobi的应用案例:TSP
第38篇:浅谈 | P问题、NP问题、NPC问题、NP-Hard问题
第35篇:优化|高级建模方法(Gurobi):线性化表达小技巧
第34篇:深度强化学习介绍 | Deep Q Network——理论与代码实现
第32篇:优化 | Pick and delivery problem的简介与建模实现(一)
第30篇:“Learn to Improve”(L2I):ICLR文章分享 | 运用RL解决VRP问题
第29篇:线性规划求解小程序 | 基于Python 的Cplex 求解器图形化界面
第27篇:Julia安装与配置Jupyter Notebook
第26篇:期刊征文| IEEE TRANSACTIONS应对COVID-19的特刊征文消息速递
第25篇:两阶段随机规划(Two-stage Stochastic Programming):一个详细的例子
第23篇:Python调用Gurobi:Assignment Problem简单案例
第20篇:运筹学与管理科学TOP期刊揭秘 —Service Science
第19篇:手把手教你用Python实现Dijkstra算法(伪代码+Python实现)
第18篇:运筹学与管理科学大揭秘—TOP期刊主编及研究方向一览
第17篇:优化 | 手把手教你用Python实现动态规划Labeling算法求解SPPRC问题
第16篇:代码 | 运小筹GitHub项目上线啦,快来标星收藏吧!!
第14篇:优化| 手把手教你用Python实现Dijkstra算法(附Python代码和可视化)
第13篇:优化|手把手教你用Python调用Gurobi求解最短路问题
第11篇:优化| 手把手教你用Python调用Gurobi求解VRPTW
第10篇:优化 | 两阶段启发式算法求解带时间窗车辆路径问题(附Java代码)
第7篇:优化 | TSP中两种不同消除子环路的方法及Callback实现(Python调用Gurobi求解)
第6篇:元启发式算法 | 禁忌搜索(Tabu Search)解决TSP问题(Python代码实现)
第5篇:论文代码复现 | 无人机与卡车联合配送(Python+Gurobi)
第4篇:优化|Shortest Path Problem及其对偶问题的一些探讨(附Python调用Gurobi实现)
第3篇:可视化|Python+OpenStreetMap的交通数据可视化(二):OpenStreetMap+Python画城市交通路网图
第1篇:Python+networkX+OpenStreetMap实现交通数据可视化(一):用OpenStreetMap下载地图数据
作者:徐璐,清华大学,清华大学深圳国际研究生院,清华-伯克利深圳学院,硕士在读
作者:刘兴禄,清华大学,清华大学深圳国际研究生院,清华-伯克利深圳学院,博士在读
审校&编辑:张瑞三,四川大学,硕士在读
初次完稿日期:2022.10.12
编辑于 2022-10-13





